「プログラミングのための確率統計」を読む : 3章 #1

離散値の確率分布

  • 確率論の基本
    • 運次第で揺らぐ値の、
      • 平均的にはどんな値がでるのかが期待値
      • 値のばらつき具合が分散
    • 大数の法則は、「揺らぐ値でもたくさん集めて平均すればゆらがなくなる」という性質

２項分布

  • 「確率pで表が出るようなコインをn回投げたとき表が何回出るか」の分布
  • 7回コインを投げる。そのうち３回表がでる確率P(X = 3)は
    • 表が出る確率 0.5
    • 裏が出る確率 0.5
      • 例えば、3連続で表が出て、その後、4連続で裏が出るなら、
      • ( 0.5 * 0.5 * 0.5 ) * ( 0.5 * 0.5 * 0.5 * 0.5 )
      • このようなパターンが 7個のコインから3個を選ぶ組み合わせ分ある。 　　 - 35 * ( 0.5 * 0.5 * 0.5 ) * ( 0.5 * 0.5 * 0.5 * 0.5 )

「プログラミングのための確率統計」を読む : 2章 #4

2.5 独立性

  • 「独立性」とは、「XとYの間に全く関わりがない」ということ。

  • P(▲▲|○○) = P(▲▲|○○でない)ということ。

  • 事象の独立性も確率変数の独立性も同じように言い換えられる

    • P(▲▲|○○) = P(▲▲|○○でない)
    • P(▲▲|○○) = P(▲▲)
    • P(▲▲,○○) : P(▲▲,○○でない) = P(▲▲でない,○○でない) : P(▲▲,○○でない)

    • P(▲▲,○○) = P(▲▲)P(○○)

    • 条件付き分布が条件によらない　:　P(X=▲|Y=○)が○に依存せずに決まる

    • 条件をつけてもつけなくても分布がかわらない　:　P(X=▲|Y=○) = P(X=▲)がどんな▲○でも常に成り立つ
    • 同時確率の比が一定　:　P(X=▲,Y=○) : P(X=▲,Y=▫️) = P(X=☆,Y=○) : P(X=☆,Y=▫️)
    • P(X=▲,Y=○) = P(X=▲)P(Y=○)が常に成立 　 - 例えばP(X = a,Y = b) = (a + 1)(b + 1)はaとbが別の項に分かれるので、XとYは独立

「プログラミングのための確率統計」を読む : 2章 #3

2.4 Byesの公式

  • P(X = ▲)・・・原因が▲の確率
  • P(Y = ○|X = ▲)・・・原因が▲のときに結果が○となる条件付き確率

このふたつから、

  • P(X = ▲|Y = ○)・・・結果が○だったときに原因が▲となった条件付き確率

を求める。

  • 結果が○となるすべての同時確率を足し合わせた確率の中の、原因が▲である割合が、P(X = ▲|Y = ○)となる。

例えば、

  • 100人のうち、５人が癌。
  • 癌発見システムは10回に1回は誤診する。
  • 癌発見システムがある人を「癌ではない」と判断した場合、その人が本当は癌である確率は？

f:id:stokutake:20151011111348p:plain

  • P(X = 癌) = 5/100
  • P(X = 癌でない) = 95/100

f:id:stokutake:20151011112229p:plain

  • 癌発見システムが癌でない人を、癌でないと判定する確率は、P(X = 癌でない) * 9/10 = 95/100 * 9/10
  • 癌発見システムが癌の人を、癌でないと判定する確率は、P(X = 癌でない) * 9/10 = 5/100 * 1/10
  • (5/100 * 1/10) + (95/100 * 9/10) = 0.86
  • 全体の0.86が癌でないと判定される。したの紫色の部分。

f:id:stokutake:20151011113434p:plain

この紫のうち、本当の癌の人は、赤の部分。つまり (5/100 * 1/10) / 0.86 = 0.00581

f:id:stokutake:20151011113648p:plain

  • 全体の中から、条件a(癌である)である結果x(癌でないと判定)になる確率、条件b(癌でない)である結果x(癌でないと判定)になる確率、・・・とすべて出して、足し合わせて、あらゆる条件で結果x(癌でないと判定)になる確率を出す。
  • その確率の中で、条件a(癌である)の場合の割合を出す。

pandasとmatplotlibでcsvデータを分析する

分析対象のデータは、日本統計学会公式認定 統計検定２級対応 統計学基礎の練習問題を一部加工。

day,Temperature,humidity,sunlighth,Wind
1,6.6,33.0,7.9,NorthWest
2,7.0,41.0,8.4,NorthNorthWest
3,5.9,48.0,5.2,NorthNorthWest
4,6.3,40.0,8.4,NorthWest
5,7.3,39.0,7.4,SouthWest
6,6.5,34.0,6.7,NorthWest
7,4.0,25.0,9.2,NorthWest
8,5.9,33.0,9.2,NorthNorthWest
9,6.1,46.0,9.1,EastNorthEast
10,3.4,27.0,9.2,NorthNorthWest
11,3.8,31.0,6.7,NorthNorthWest
12,5.1,37.0,8.4,NorthNorthWest
13,4.4,28.0,8.6,NorthNorthWest
14,3.8,36.0,9.1,WestNorthWest
15,4.0,52.0,1.1,EastNorthEast
16,2.2,39.0,8.2,NorthNorthWest
17,5.0,26.0,8.7,NorthNorthWest
18,5.5,36.0,9.4,NorthWest
19,6.3,41.0,9.3,NorthNorthWest
20,5.4,31.0,9.4,NorthNorthWest
21,5.0,28.0,9.3,NorthWest
22,6.0,34.0,9.4,NorthNorthWest
23,5.7,42.0,6.3,SouthEast
24,5.1,65.0,3.5,NorthWest
25,5.9,34.0,8.6,NorthWest
26,5.3,37.0,7.3,NorthWest
27,5.5,28.0,8.0,NorthNorthWest
28,3.7,30.0,9.3,NorthNorthWest
29,4.2,40.0,7.8,NorthNorthWest
30,2.9,34.0,5.1,NorthWest
31,2.9,28.0,9.7,WestNorthWest

風向きWindの度数と相対度数を棒グラフ化

import pandas as pd
import matplotlib.pyplot as plt

data = pd.read_csv("/Users/technote/Documents//weather.csv", encoding='Shift_JIS')

n = float(data["day"].count())
frequency = data.groupby('Wind')['day'].count().apply(lambda x: pd.Series([x], index=['frequency']))
relative_frequency = data.groupby('Wind')['day'].count().apply(lambda x: pd.Series([x / n], index=['relative frequency']))

frequency.plot(kind='bar')
relative_frequency.plot(kind='bar')

plt.show()

  • 度数 f:id:stokutake:20151010144957p:plain

  • 相対度数 f:id:stokutake:20151010145000p:plain

平均気温の度数分布表と棒グラフ

  • 階級を1度に設定する。
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

data = pd.read_csv("/Users/workspace/PSCS/weather.csv", encoding='Shift_JIS')

n = float(data["day"].count())
frequency = data.groupby('Temperature')['day'].count().apply(lambda x: pd.Series([x], index=['frequency']))

c = pd.cut(frequency.index, np.arange(1, 10, 1))

classfied_frequency = frequency.groupby(c).sum()

print classfied_frequency

classfied_frequency.plot(kind='bar')

plt.show()
  • 度数分布表
       frequency
(1, 2]        NaN
(2, 3]          3
(3, 4]          6
(4, 5]          4
(5, 6]         11
(6, 7]          6
(7, 8]          1
(8, 9]        NaN
  • 棒グラフ

f:id:stokutake:20151010151356p:plain

平均気温の箱ヒゲ図

import pandas as pd
import matplotlib.pyplot as plt

data = pd.read_csv("/Users//PSCS/weather.csv", encoding='Shift_JIS')

temp = data[['Temperature']]

temp.boxplot(return_type='axes')

plt.show()

f:id:stokutake:20151010162615p:plain

気温と湿度の相関

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt

data = pd.read_csv("/Users/tokutake/Documents/workspace/PSCS/weather.csv", encoding='Shift_JIS')

r = np.corrcoef(data['Temperature'], data['humidity'])[0, 1]

plt.scatter(data['Temperature'], data['humidity'])

plt.title('r=%.2f' % r, size=16)
plt.xlabel('Temperature', size=14)
plt.ylabel('humidity(%)', size=14)

plt.show()

f:id:stokutake:20151010170039p:plain

分布について : t分布

t分布

f:id:stokutake:20151004125629p:plain

  • 正規母集団から「データをn個、((取り出した値n個の平均 - 母平均) / 取り出した値n個の標準偏差) * (n - 1) を計算する」ということを何度も繰り返す。
  • この値n-1の自由度で t分布する。

  • t分布の数表は明らかなので、母集団の平均を推定できる。

  • 正規母集団から、５人の身長を取り出す。

  • 172cm,162cm,159cm,177cm,155cm
  • 母平均を推定する。
  • 標本平均は、165cm
  • 標本分散は、'(172 - 165)2 + (162 - 165)2 + (159 - 165)2 + (177 - 165)2 + + (155 - 165)2) / (5 - 1) = 84.5
  • 標本標準偏差は、9.19
  • -2.776 ≦ ((165 -μ) / 9.19) * 4 ≦ 2.776
  • 95%信頼区間は、158.6 ≦ μ ≦ 171.3

分布について : カイ２乗分布、標本から母分散の推定する(母平均がわかっている場合)

カイ２乗分布

https://upload.wikimedia.org/wikipedia/commons/thumb/2/21/Chi-square_distributionPDF.png/1024px-Chi-square_distributionPDF.png

  • 正規母集団から「データをいくつか取り出して、(取り出した値 - μ) / σ の２乗和を計算する」ということを何度も繰り返す。
  • この値 Vはカイ２乗分布する。

  • 分布の数表によれば、0.21 ≦ v ≦ 9.34 の範囲に95%のデータが入る。

  • 例えば、芋虫の母集団の体長が平均10cmで、正規分布する場合

  • この母集団から「５匹の芋虫を取り出して,(取り出した値 - μ) / σ の２乗和を計算する」ということを何度も繰り返す。
  • この値 Vはカイ２乗分布する。
  • 何度も繰り返すうちの１回の現実に観測された体長が、9cm,8cm13cm,16,cm,18cmの場合、現実に観測されたvは114/σ２乗
  • この値が、0.21 ≦ v ≦ 9.34 の範囲にはいらないようなσは母分散として不適切。
  • 計算すると12.2 ≦ σ２乗 ≦ 23.94。

分布について : 正規分布と標準正規分布、標本から母平均の推定する(標準偏差がわかっている場合)

分布するということ

  • まちまちの値をとるということ。

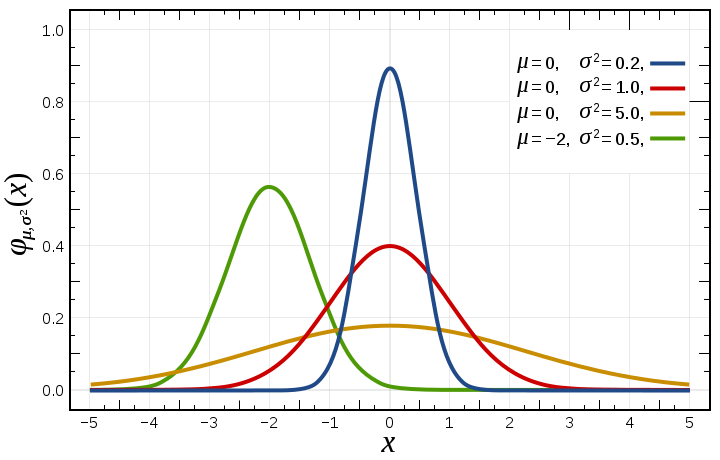
正規分布

  • 平均を頂点とした釣鐘型の分布

https://upload.wikimedia.org/wikipedia/commons/thumb/7/74/Normal_Distribution_PDF.svg/720px-Normal_Distribution_PDF.svg.png

正規分布の標準化

  • 正規分布のそれぞれの値から平均値をマイナスし、標準偏差で除算。
  • (x- μ) / σ
  • この値の分布が平均0、標準偏差1の分布になる。これが、標準化された正規分布。標準正規分布
  • (x- μ)を偏差という。偏差の合計は0になるので、標準正規分布の平均は0になる。
  • σで除算することで(x- μ)が標準偏差の何倍かがわかる。つまり、その値がどのくらい月並みか特殊化がわかる。

https://upload.wikimedia.org/wikipedia/commons/thumb/8/8c/Standard_deviation_diagram.svg/400px-Standard_deviation_diagram.svg.png

  • 例えば、17歳男子の平均身長170.7 標準偏差 5.79 の場合
    • 182cmの男子の(x- μ) / σ は (182- 170.7) / 5.79 = 1.951
    • つまり、標準偏差の約1.95倍
    • 2倍近いので比較的特殊。
    • 95%の(x- μ) / σが、-1.96 ≦ (x- μ) / σ ≦ 1.96 の範囲に収まる。
    • 1.95はぎりぎり95%に収まっている

標本平均の分布

  • 正規母集団から「データをいくつか取り出して平均を算出する」ということを何度も繰り返す。
  • そうすると標本平均の分布ができる。
  • この分布も正規分布する。
  • この分布の平均、つまり、標本平均の平均は母集団の平均になる。

  • この分布の標準偏差は母集団の標準偏差σをデータの個数のルートで割ったものになる。

  • 河原のすべての石の重さが正規母集団で、標準偏差が20グラムだとする。

    • 25個の石を拾って重さを平均したら、80グラムだった。
    • 「25個の石を拾って重さを平均する」を何度も繰り返して取得した平均は正規分布する。
    • この分布の平均は母集団の平均μである。
    • この分布の標準偏差は母集団の標準偏差20をデータの個数のルート、√25で割った値、つまり、4である。
  • 母集団の平均を区間推定してみる。
  • 「25個の石を拾って重さを平均する」を何度も繰り返して取得した平均の正規分布を標準化する。 　- ((「25個の石を拾って重さを平均する」を何度も繰り返して取得した平均X) - 母集団の平均μ ) / (この分布の標準偏差4) の分布が標準正規分布になる。
    • この標準正規分布もその特性上、-1.96 ≦ (X- μ) / 4 ≦ 1.96の範囲に値が収まる。Xはまちまちの値をとり、値によって、 (X- μ) / 4 が 1.96より大きくなったり小さくなったり、-1.96より大きくなったり小さくなったりする。
    • 実際に観測された標本平均80を代入すると、-1.96 ≦ (80- μ) / 4 ≦ 1.96。この式が成り立たないμは、現実の母集団の平均値として不適切であると考える。
    • 72.16 ≦ μ ≦ 87.84
    • μは95%の確率で72.16以上、87.84以下